跳至内容
【概率规律】一个排列组合问题答案深入研究,规律行走路线
这篇文章的起源是备课时被一道题目卡住了,看过答案之后,觉得里面的某些文字还是不太理解,于是探究了一番,姑且得到了能让学过排列组合基础知识的孩子们能理解的讲述方法,所以记录在此。“解答再探”这种继续研究答案细节的文章,以后可能会做成一个系列。
用A、B、C、D、E、F六种燃料去染下图的两个调色盘,要求每个调色盘里的六种颜色不能相同,且相邻四种颜色在两个调色盘里不能重复,那么共有______种不同的染色方案(旋转算不同方法)。
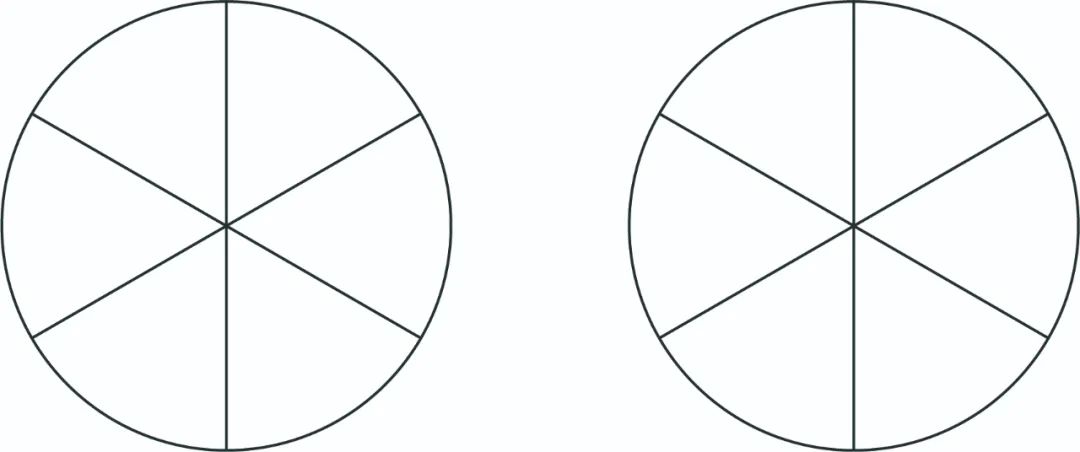
顺便说,“六种燃料”可能是错别字,正确说法可能是“六种染料”。
即使是再研究答案,也得先理解题意。题目说用六种染料去染下图的两个调色盘,那就是染色问题。接着说“要求每个调色盘里的六种颜色不能相同”,这句话得具体琢磨琢磨,是“每个调色盘”里的六种颜色不能相同,那第一个调色盘中,就只能是A,B,C,D,E,F六个颜色都要用到,这样才能做到“六种颜色不能相同”,第二个调色盘也是这样,由此能联想到的是,这就得用“排序”来区分染色种类的不同了。
接下来是“且相邻四种颜色在两个调色盘里不能重复”,拆解一下,是“相邻四种颜色”,在“两个调色盘”里,不能重复,举个例子比较好理解。比如第一盘中有颜色ABCD连续,第二盘中就不能出现ABCD连续的情况。
然后是问题,共有多少种不同的染色方案。还有括号里的文字,“旋转算不同方法”,这句话也可以举例子理解,无非就是:
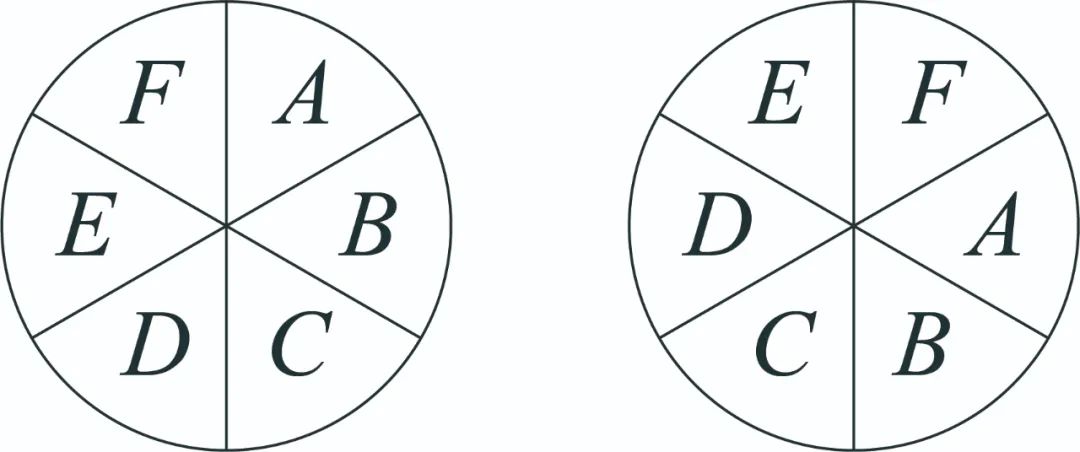
因为是答案再研究,所以看看解答怎么说。(解答来自网络)
【答案】 在一个调色盘里有有6×5×4×3×2×1=720种染法;再看另外一个调色盘,相邻的四种颜色重复分为4个重复,5个重复和6个重复,由于5个重复6个就必然重复,所以只要分4和6两种就行了.4种颜色重复有6种情况,6种颜色重复。
【解析】 由于有两个调色盘,先在两个调色盘中选一个,则在这个调色盘里有6×5×4×3×2×1=720种染法,再看另外一个调色盘,相邻的四种颜色重复分为4个重复,5个重复和6个重复,但由于5个重复6个就必然重复,所以只要分4和6两种就行了。4种颜色重复有6种情况,6种颜色重复只有1种。每种情况经旋转可变出6种。所以共有6×5×4×3×2×1-1×6-6×6=678。总共有678×720=488160种。
阅读一下就知道,虽然分为【答案】和【解析】,但【答案】更像解析,【解析】更像答案,而且两部分文字重复内容也比较多,所以只看【解析】就可以。
【解析】开始的话好理解,“由于有两个调色盘,先在一个调色盘里染色”,6个格的颜色互不相同,所以一共有:
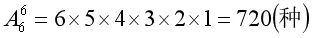
接着说的是,“再看另一个调色盘”,这也好理解,因为两个调色盘有“不能相同”的部分,所以先确定一个的染色方法,再确定另一个。然后是“相邻的四种颜色重复分为4个重复,5个重复和6个重复”,这句话属于“看起来好像是懂了,但如果深究的话不一定懂”的类型,具体分析一下,这里说的“4个重复,5个重复和6个重复”其实应该是“只有4个相邻格重复”,“只有5个相邻格重复”和“只有6个相邻格重复”,因为仅“4个重复”这几个字,是可以包含在4个相邻格重复的基础上共有5个格或者6个格重复的,所以在此要理解得更详细些。“重复”具体指的是第二个调色盘和第一个调色盘有4个相邻格相同的情况。比如:
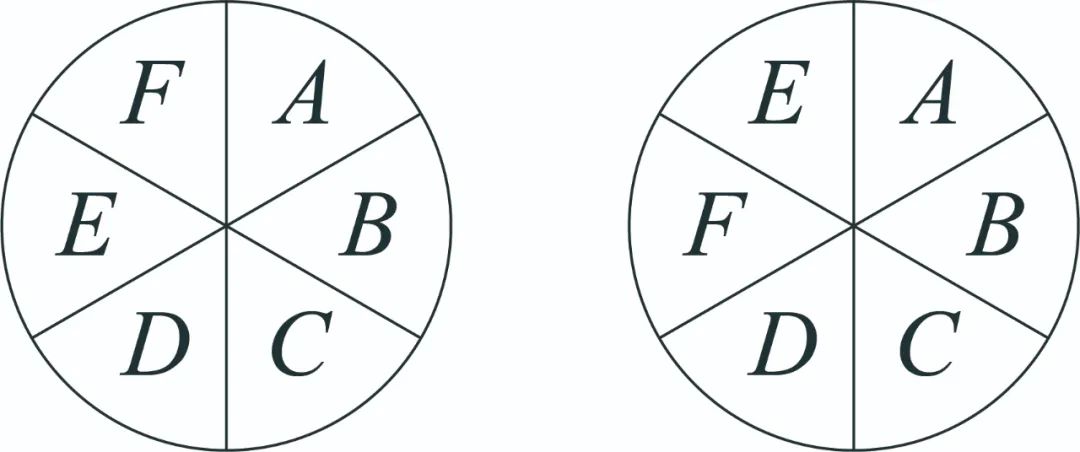
“但由于5个重复6个就必然重复”,这句话说的是当第二调色盘中有5个格的颜色和第一调色盘中5个格的颜色相同时,也就等同于6个格的颜色相同,因为只有6个格,只有6个不同颜色。
“所以只要分4和6两种就行了”很好理解,因为“5个重复”和“6个重复”完全一样,所以统计染法时看作一种就可以。
接下来是计算过程,“4种颜色重复有6种情况”。我刚看到这句话是确实是感觉“对对对,是这样”,不过想到怎么跟孩子们说能更明白时,就不知道该怎么说了,所以其实我还是没明白,得具体研究,也就是为什么4种颜色重复时有6种情况(6种染法)。
还是提示一下自己,“4种颜色重复”指的是“第二个调色盘中只有4个相邻格的颜色和第一个调色盘中的4个相邻格颜色相同”,还是举个例子好理解。
再具体分析一下,上图中,以中间的竖直线段为分割线,从上方右侧字母A开始,逆时针绕行,分别为A,B,C,D,E,F,如果我们规定“A,B,C,D”为“4个相邻格且颜色相同”,左侧调色盘不动,右侧调色盘中原“E,F”的位置,就必须变成E在上,F在下了。如果是另外一种情况,即F在上,E在下,那就和左侧调色盘完全一样,这就不属于“4种重复”,而是“6种重复”。
插个话,如果这样的话,好像可以把“4种重复”和“6种重复”一起统计,不用分开。不过在此,还是按照答案来分析。
答案说的“4种颜色重复有6种情况”,我们刚刚找到了1种。然后看看第2种是什么。因为刚才我们锁定了A,B,C,D的组合以及顺序不动,所以要和左侧调色盘保持“4个重复”,好像就只能换锁定的组合了。那就按照逆时针转着来,这次锁定B,C,D,E,那剩余的F,A就要和左侧调色盘不同,变成这样:
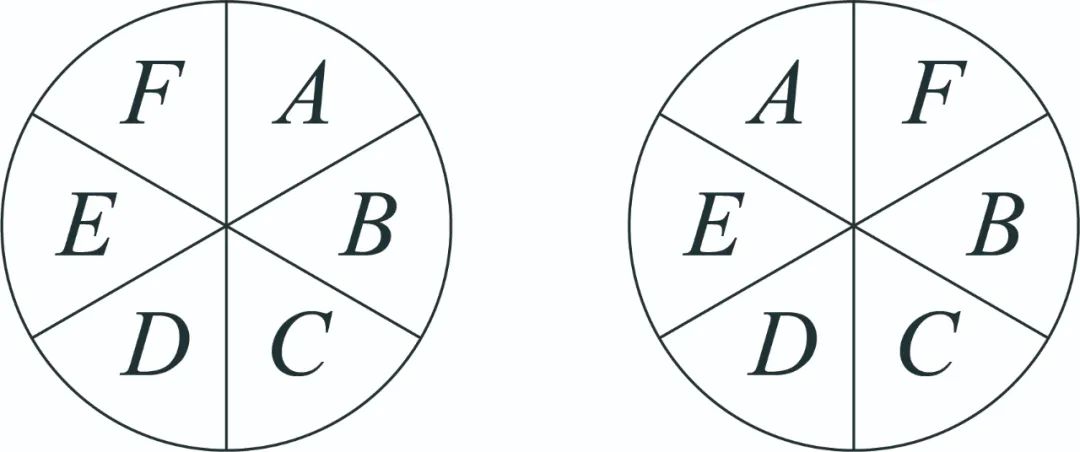
因为刚才寻找“4种重复”的方式有规律,有顺序,所以继续操作就可以,找到6种情况:
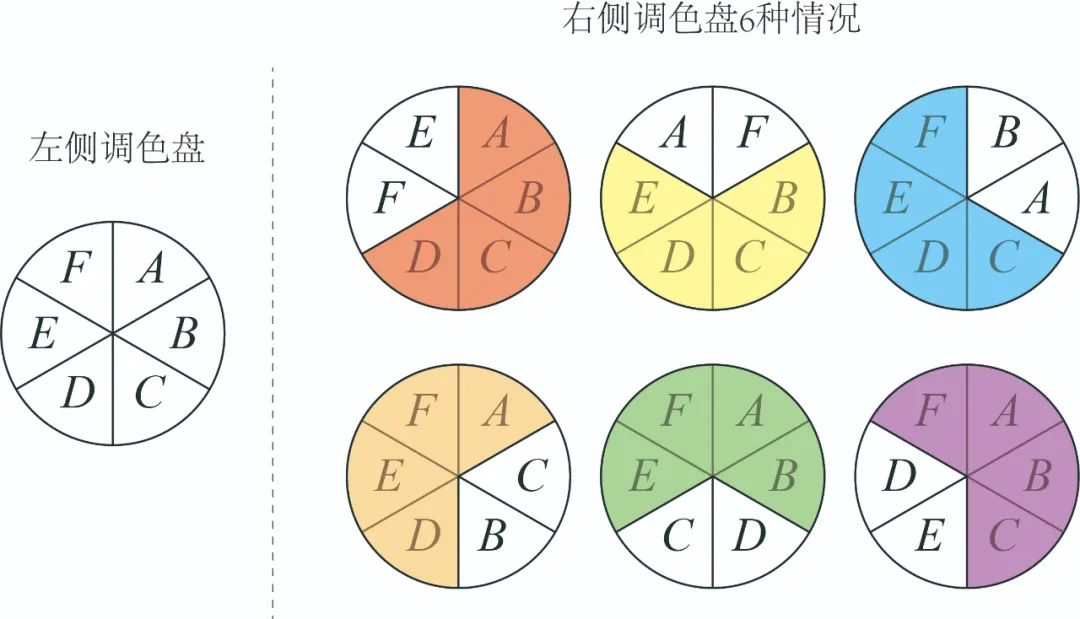
然后是“6种颜色重复只有1种”,这个很好理解,就是右侧调色盘和左侧完全一样,所以是1种:
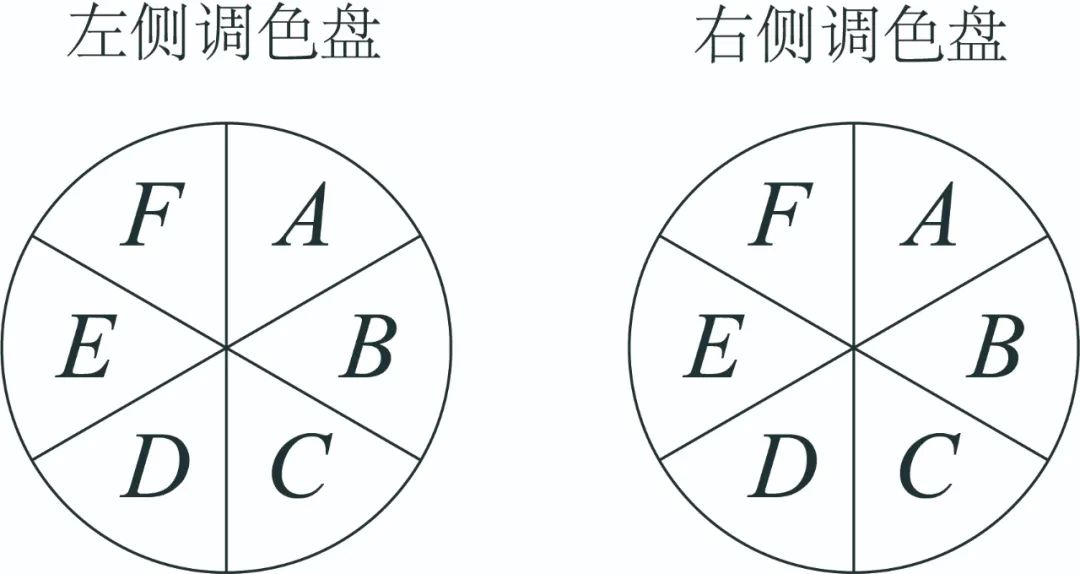
后面的那句话有点歧义,说的是“每种情况经旋转可变出6种”,注意【解析】中这句话前面的句号,指的是“4种重复”的6种情况,和“6种重复”的1种情况,都可以旋转变出6种。这也对应后面的算式:
“所以共有6×5×4×3×2×1-1×6-6×6=678”中“-1×6-6×6”,1种和6种每个数都乘以了6。
那就牵扯到一个问题,问什么要旋转,为什么旋转之后可以有6种情况。
如果刚开始想不明白,可以先旋转一下看看,还是左侧调色盘不动,右侧转一下:
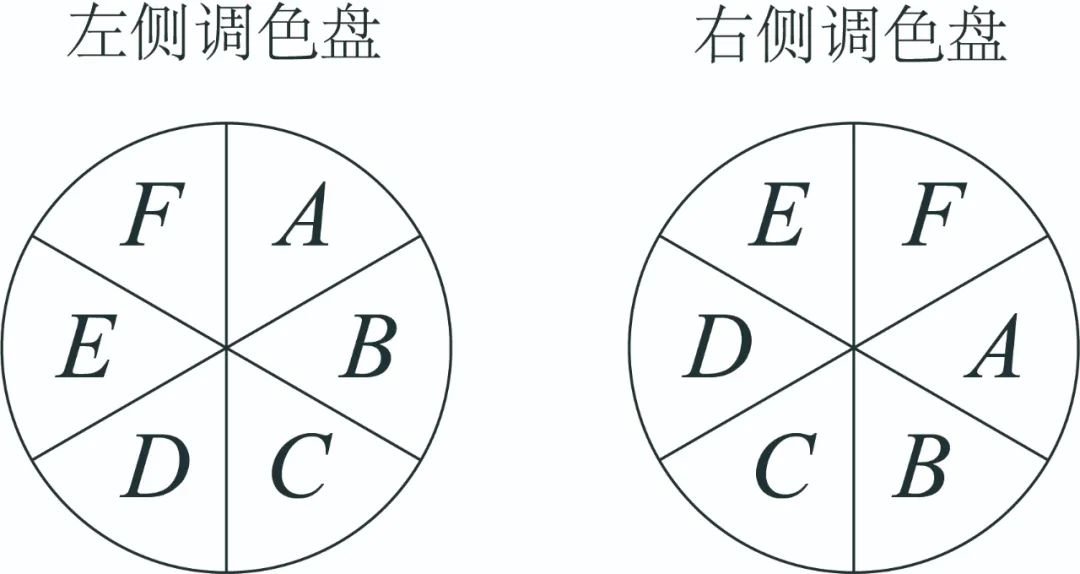
这属于“6种重复”对应的“1种”,旋转之后的样子,按照【解析】的说法,它算作“6种重复”的1种,旋转变出来的第1种。但目前看起来,好像也不能算作1种。这个位置我也确定了挺长时间,然后我看了下题目原文的一句话“且相邻四种颜色在两个调色盘里不能重复”,也就是说,只要右侧调色盘里出现“相邻四种颜色在两个调色盘里重复”,就要去掉,所以这句话指的是两个调色盘的“相对位置”,决定性因素不是位置不一样所以不能算作“6种重复”,而是只要是按照“ABCDEF”的顺序排在一起相邻,就算做相同。所以,在此可以确定“6种重复”的1种,可以旋转变出1×6=6种:
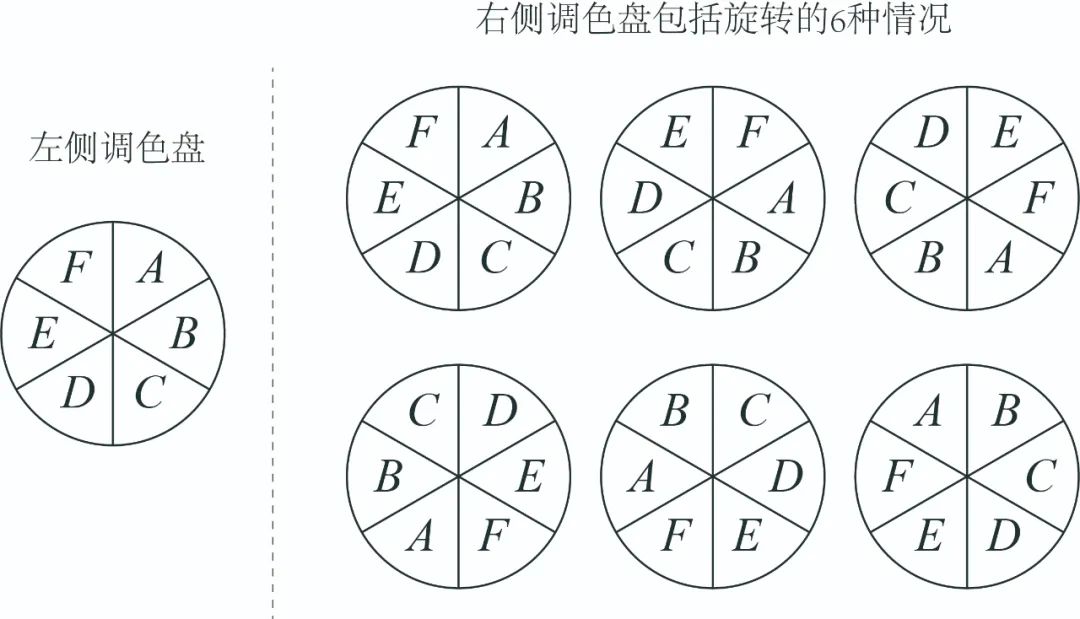
照此推理方式,“4种重复”中的每1种,也可以经过旋转,变出6种:
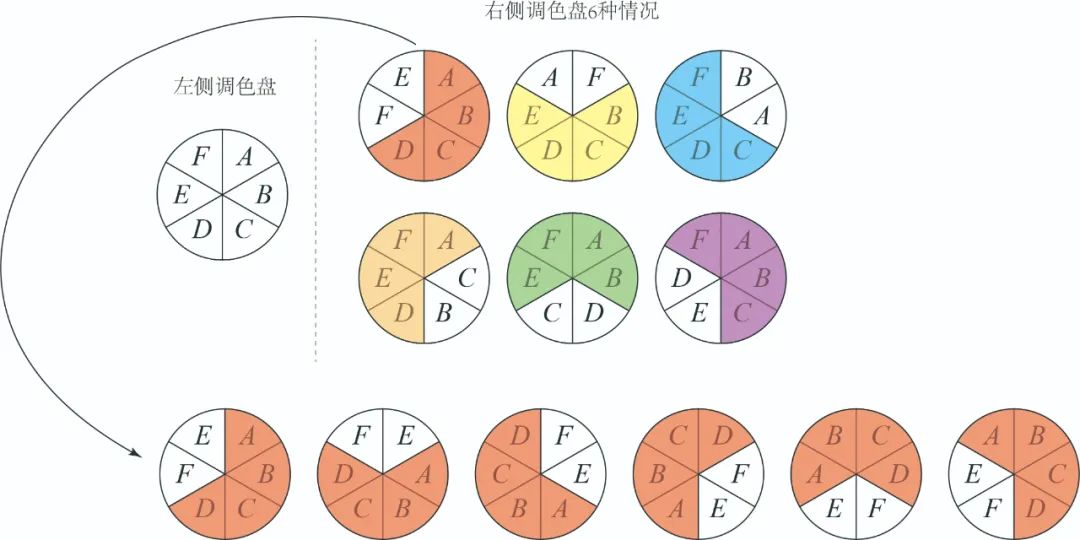
类似地,“4种重复”的其它5种情况也都可以分别衍生出6种,所以一共是6×6=36种。
再所以,以上的6种和36种都属于“且相邻四种颜色在两个调色盘里重复”的情况,所以要去掉。然后看看【解析】的最终算式:
所以共有6×5×4×3×2×1-1×6-6×6=678。总共有678×720=488160种。
第一个算式好理解一些,说的就是右侧调色盘,逻辑是“全部情况减掉不符合条件的情况”,不符合条件的就是刚才计算的6种+36种共42种,全部情况是右侧调色盘的全排列,也就是不考虑与左侧调色盘重不重复的所有可能,即右侧调色盘满足条件的有:
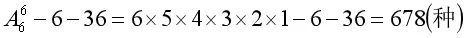
接下来解决最后一个问题,为什么“总共有678×720=488160种”中是678“乘以”720?
首先,720种来自于左侧调色盘的所有可能,也就是左侧调色盘一共有720种染色方式,而右侧调色盘是根据题意搭配左侧调色盘的,所以意味着左侧调色盘的每一种染色方式,都会搭配右侧调色盘678种染色方式,所以就是720×678种,即:
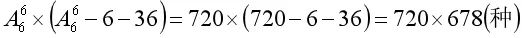
整体分析一遍,其实有助于我们了解每一步的细节,也能更深入理解“排列组合”公式和算法的意义,同时也能在解决其它题目时引发灵感。

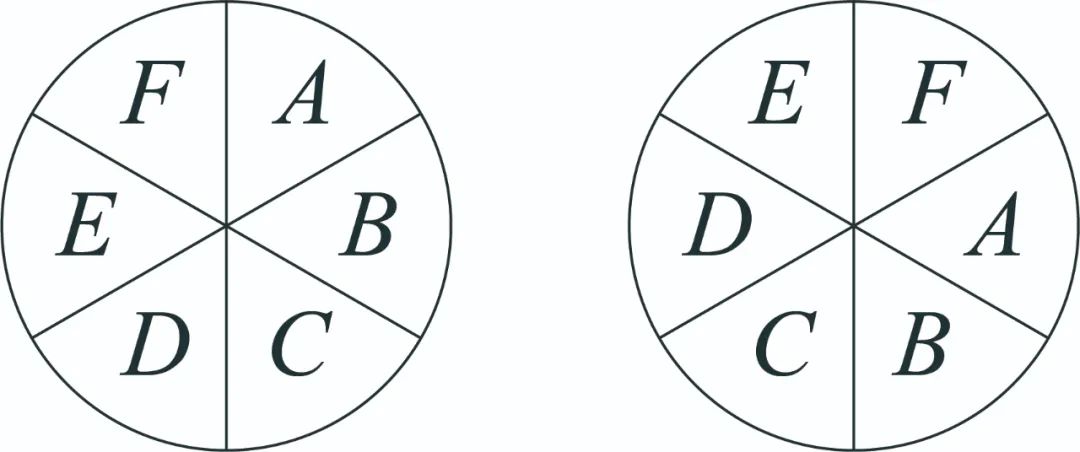
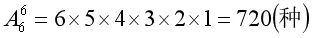








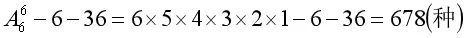
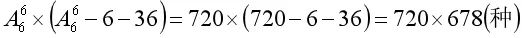

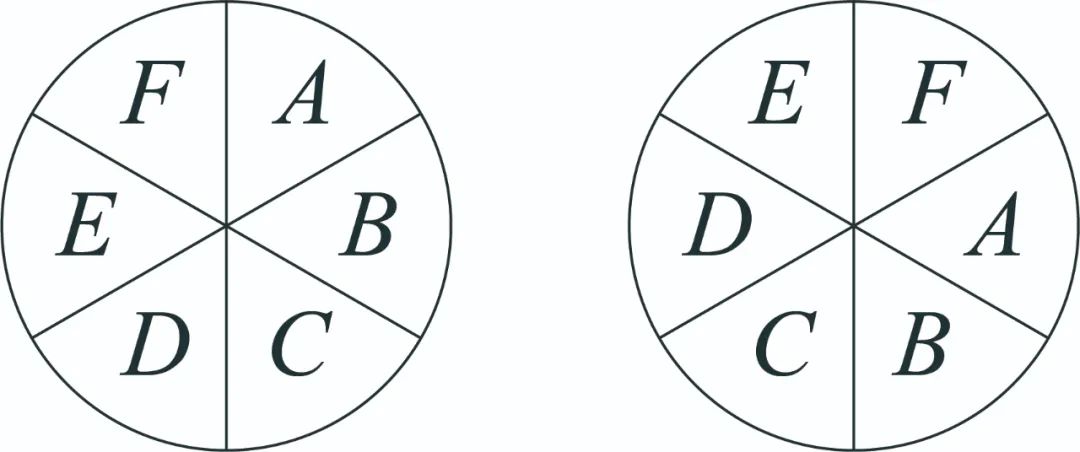
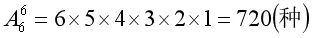








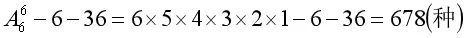
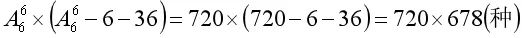
点赞《【概率规律】一个排列组合问题答案深入研究,规律行走路线》文章
点赞《【概率规律】一个排列组合问题答案深入研究,规律行走路线》文章
收藏《【概率规律】一个排列组合问题答案深入研究,规律行走路线》文章
收藏《【概率规律】一个排列组合问题答案深入研究,规律行走路线》文章
点赞《【概率规律】一个排列组合问题答案深入研究,规律行走路线》文章
收藏《【概率规律】一个排列组合问题答案深入研究,规律行走路线》文章
点赞《【概率规律】一个排列组合问题答案深入研究,规律行走路线》文章